Menu
July 23, 2024 By Sadia Khan 5 minutes read
Have you ever wondered why some processes in nature seem to happen spontaneously while others require a push? That’s where entropy comes into play. In this article, we’ll dive deep into the concept of entropy, a fundamental idea in both thermodynamics and information theory. We’ll explore its definition, core concepts, and the significant impact it has across various fields, including engineering, environmental science, and information technology.
Whether you’re a student just starting out or a seasoned engineering professional, this guide will help you understand why entropy is such a crucial concept.
Entropy is a measure of the randomness or disorder within a system. It’s a fundamental concept in thermodynamics that helps explain why certain processes occur spontaneously while others do not.
Imagine you have a box divided into two compartments. One compartment is filled with gas molecules, while the other is empty. If you remove the divider, the gas molecules will naturally spread out to fill the entire box.
This process increases the entropy of the system because the molecules are now more randomly distributed. Initially, the gas molecules were confined to one side, representing a state of lower entropy (more order).
After removing the divider, the molecules disperse, leading to a state of higher entropy (more disorder).
The term “entropy” was first introduced by the German physicist Rudolf Clausius in the mid-19th century. Clausius was working on the principles of thermodynamics, the science of heat and energy transfer. He coined the term from the Greek word “trope,” meaning transformation, to describe the measure of energy dispersion in a system.
But Clausius wasn’t the only one involved. Ludwig Boltzmann, an Austrian physicist, made significant contributions by linking entropy to a system’s microscopic states.
In the 20th century, Claude Shannon, an American mathematician and electrical engineer, extended the concept of entropy into the realm of information theory.
Shannon’s entropy measures the uncertainty or information content in a message, revolutionizing the fields of communication and data science.
In thermodynamics, entropy measures the randomness or disorder within a system. It’s often used to quantify the irreversibility of natural processes.
Imagine you have a hot cup of coffee. Over time, it cools down to room temperature. This process is irreversible—once the coffee has cooled, it won’t spontaneously heat back up. Entropy helps us understand why.
The mathematical representation of entropy (S) in thermodynamics is given by:
Entropy is given as:
Where,
ΔS = Change in entropy
dQ = Infinitesimal amount of heat added to the system, and
T = Absolute temperature at which the heat is added.
Entropy increases when heat is added to a system at a certain temperature. This increase in entropy corresponds to a greater degree of disorder or energy dispersal within the system.
The Second Law of Thermodynamics is one of the cornerstones of entropy. It states that in any natural process, the total entropy of a closed system will either increase or remain constant; it never decreases.
This law implies that energy transformations are not 100% efficient, and some energy is always dispersed as heat, increasing the system’s entropy.
For example, consider a steam engine. When steam expands to move a piston, not all the energy from the steam is converted into mechanical work. Some of it is lost as heat, which disperses into the surroundings, increasing the overall entropy.
From the statistical mechanics viewpoint, entropy is related to the number of microscopic configurations (microstates) that correspond to a system’s macroscopic state (macrostate).
The more microstates available, the higher the entropy. Boltzmann’s entropy formula beautifully encapsulates this idea:
S=k B ln Ω
= entropy
k is Boltzmann’s constant
Ω = Omega is the number of microstates.
Think of it like this: if you have a set of building blocks and arrange them in a specific pattern, there are many ways to rearrange the blocks while still achieving the same overall structure.
Each unique arrangement represents a microstate, and the overall structure is the macrostate. More possible arrangements (microstates) mean higher entropy.
Claude Shannon’s work brought a new dimension to entropy, which measures the uncertainty or unpredictability of information content in information theory.
This is crucial in data compression and transmission. Shannon entropy is defined as:
Shannon entropy quantifies the amount of “surprise” in a set of possible messages. Higher entropy means more unpredictability, which is vital for efficient data encoding and error detection in communication systems.
A common misconception is that Entropy is simply a measure of disorder. While it is true that Entropy often increases with disorder, a more accurate description is that Entropy measures the dispersal of energy.
For example, when ice melts into water, the orderly crystal lattice of ice breaks down, and the molecules move more freely, leading to higher Entropy.
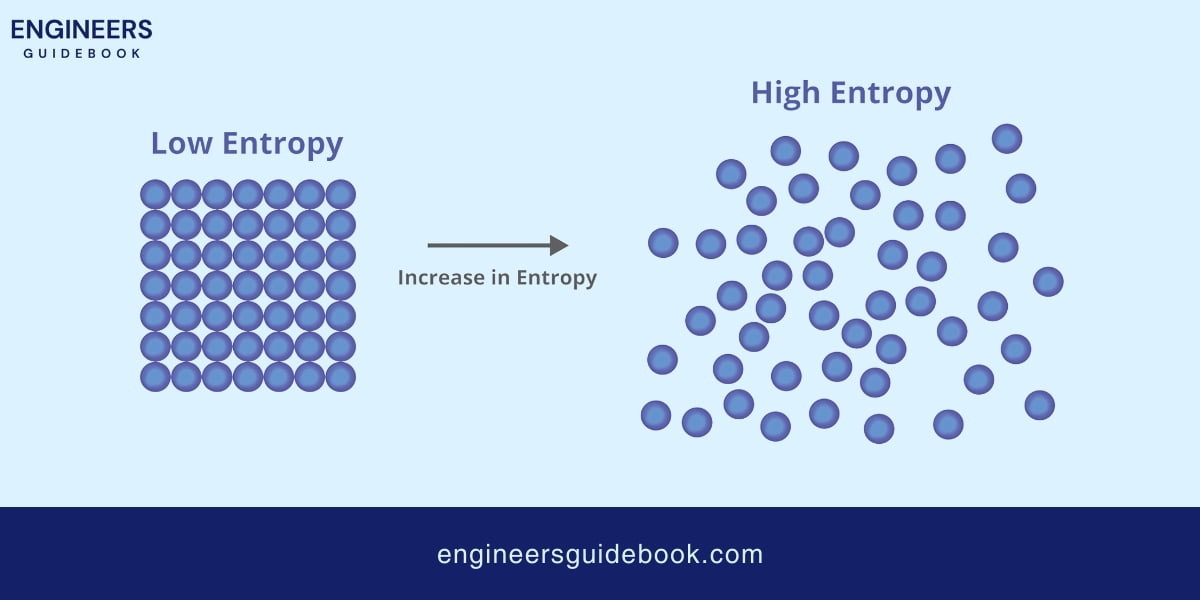
However, the rise in Entropy is truly characterized by the increased freedom of molecular movement (energy dispersal).
Entropy behaves differently in closed and open systems. In a closed system, where no energy or matter is exchanged with the surroundings, the total Entropy can only increase or stay the same, never decreasing.
However, in an open system, Entropy can decrease locally as long as the total Entropy of the system and its surroundings increases.
In an isothermal process, the temperature remains constant. The entropy change (ΔS\Delta S) for such a process can be calculated using the formula:
ΔS=Q / T
ΔS = 1000J / 300K
ΔS = 3.33 J/K
In an adiabatic process, no heat is exchanged with the surroundings. Hence, the entropy change is zero for an ideal adiabatic process.
However, real processes often involve some irreversibility’s, leading to a small increase in Entropy.
During phase transitions, such as melting or boiling, the entropy change can be calculated using the latent heat (L) of the substance:
ΔS = L / T
For instance, when 1 kg of ice melts at 0°C (273 K), it requires 334,000 J of energy (latent heat of fusion). The entropy change is:
ΔS = 334,000J / 273K
ΔS = 1223J/K
Measuring Entropy directly can be challenging, but it can be inferred from other measurable properties such as temperature, pressure, and heat transfer. Here are some practical methods and instruments used:
Calorimetry is a technique for measuring the amount of heat involved in a chemical reaction or other processes. By measuring the heat exchange and knowing the temperature, the entropy change can be calculated using the appropriate formula.
Thermocouples and other temperature sensors measure system temperature changes. By integrating these measurements with heat transfer data, entropy changes can be deduced.
For many substances, entropy values at different temperatures and pressures are tabulated and available in reference books and databases. Engineers and scientists use these tables to find entropy values for various states of a substance without direct measurement.
In advanced research, specific experimental setups like adiabatic calorimeters or differential scanning calorimetry (DSC) are used to measure entropy changes with high precision.
These setups are often used in materials science and thermodynamics research to study the properties of new materials.
Entropy is fundamental to understanding the efficiency of heat engines, such as steam turbines, internal combustion engines, and refrigeration cycles.
The Second Law of Thermodynamics tells us that no engine can be 100% efficient because some energy is always lost as heat, increasing the system’s Entropy. Engineers use entropy calculations to optimize the design and operation of these engines, ensuring maximum efficiency.
In chemical engineering, Entropy is vital for predicting the direction and feasibility of chemical reactions.
The concept of Gibbs free energy, which combines Entropy and enthalpy (heat content), helps determine whether a reaction will occur spontaneously.
For instance, in the Haber process for ammonia synthesis, understanding the entropy changes helps in optimizing the reaction conditions to maximize yield.
Entropy is used to study phase transitions and the stability of materials. When designing new alloys or composites, scientists examine entropy changes to predict properties like melting points, solubility, and mechanical strength.
This knowledge is essential for developing advanced materials for aerospace, automotive, and electronic applications.
Shannon entropy is key to data compression algorithms. By quantifying the redundancy in a data set, these algorithms can compress data efficiently without losing essential information.
Techniques like Huffman coding and Lempel-Ziv-Welch (LZW) use entropy calculations to achieve optimal compression.
In cryptography, Entropy measures the unpredictability of keys and encryption algorithms. Higher Entropy means more secure encryption, as it becomes harder for attackers to predict the key or decrypt the information without authorization.
Cryptographers design systems to maximize Entropy, ensuring robust security for digital communications.
Entropy principles guide the development of energy-efficient technologies.
For example, improving building insulation reduces heat loss, decreasing the Entropy generated and conserving energy.
Similarly, optimizing industrial processes to minimize waste heat can lead to significant energy savings.
Entropy has far-reaching impacts across various domains, influencing technological advancements, economic systems, and future research directions.
Entropy is a critical factor in the development of new technologies. In renewable energy, understanding entropy helps improve the efficiency of solar panels and wind turbines.
In computing, entropy is crucial for developing efficient algorithms and enhancing data security.
Modern processors and storage devices are designed to handle data with high entropy, ensuring fast processing and robust security measures.
Similarly, in battery technology, minimizing entropy production during charge and discharge cycles enhances battery life and performance.
In economics, entropy concepts are used to analyze resource management and sustainability.
Processes that generate high entropy, such as excessive waste production, are less economically viable in the long run. By reducing entropy, industries can achieve greater efficiency and cost-effectiveness.
For example, the circular economy model aims to minimize waste by reusing and recycling materials, thereby reducing entropy production.
This approach not only conserves resources but also lowers production costs and environmental impact.
Entropy also plays a role in understanding economic systems. Markets can be viewed as complex systems where entropy measures the level of disorder or unpredictability. High entropy in financial markets indicates greater uncertainty and risk.
Economists use entropy-based models to predict market behaviors and develop strategies for risk management.
As we advance, understanding entropy will be pivotal in developing new technologies.
For instance, in the field of nanotechnology, controlling entropy at the nanoscale can lead to the creation of materials with unique properties, such as self-healing materials and ultra-lightweight composites.
In biotechnology, entropy principles guide the design of drug delivery systems that release medication in controlled, predictable ways, improving treatment efficacy and patient outcomes.
Understanding entropy is essential for anyone involved in engineering, science, or technology. From engine efficiency to data security, entropy helps explain why things happen the way they do.
As we’ve explored, entropy is not just a measure of disorder but a fundamental principle that dictates the flow of energy and information.
Whether you’re dealing with heat transfer, chemical reactions, or digital communications, a solid grasp of entropy can lead to better designs, more efficient systems, and innovative solutions to complex problems.
As we move forward into an era of rapid technological advancement and growing environmental concerns, the role of entropy in shaping sustainable practices and groundbreaking technologies will only become more significant.
By continuing to study and apply the principles of entropy, we can unlock new possibilities and drive progress in countless fields.
Entropy is a measure of the randomness or disorder in a system. It quantifies how energy is spread out or dispersed within a system.
Entropy is crucial in thermodynamics because it helps explain the direction of energy transfer. According to the Second Law of Thermodynamics, in an isolated system, entropy tends to increase, leading to the irreversibility of natural processes.
Entropy is measured in units of joules per kelvin (J/K). It can be calculated using the formula
ΔS = Q \ T
where,
Q is the heat added to the system
T is the absolute temperature.
Examples of entropy include the melting of ice into water, the spreading of a gas in a container, and the mixing of different substances. Each of these processes involves an increase in disorder and energy dispersal.
The Second Law of Thermodynamics states that the total entropy of an isolated system can never decrease over time. This law implies that natural processes tend to move towards a state of greater disorder or entropy.
In an isolated system, entropy cannot decrease. However, in an open system, entropy can locally decrease if the overall entropy of the system and its surroundings increases.
This is how living organisms maintain order internally while increasing the entropy of their environment.
In thermodynamics, entropy measures the disorder and energy dispersal in a physical system. In information theory, entropy measures the unpredictability or information content in a set of possible messages.
Despite the different contexts, both concepts quantify uncertainty and randomness.
Entropy affects the efficiency of engines and refrigerators by dictating the irreversibility of energy transformations. Higher entropy production means greater energy loss as waste heat, reducing the efficiency of these devices.
Entropy is considered a measure of irreversibility because it quantifies the amount of energy that is no longer available to do work in a system. As entropy increases, the system moves towards equilibrium, and the processes become irreversible.
Sadia Khan, a Chemical Engineering PhD graduate from Stanford University, focuses on developing advanced materials for energy storage. Her pioneering research in nanotechnology and battery technology is setting new standards in the field.
Explore the Engineer’s Guidebook! Find the latest engineering tips, industry insights, and creative projects. Get inspired and fuel your passion for engineering.
© 2023-2024 Engineer’s Guidebook. All rights reserved. Explore, Innovate, Engineer.